EECS20N: Signals and Systems

Frequency Response of Feedback Systems

Consider the feedback composition with two LTI systems:

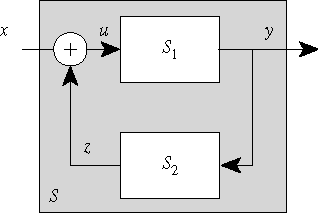
Assume the frequency response of S1 is H1, of S2 is H2, and of S is H. Then assume that

x = exp(i ω t).

The output must be

y = H(ω)x

Since this is itself a complex exponential, it must be true that

z = H2(ω)y = H2(ω)H(ω)x

Hence

u = x − z = x − H2(ω)H(ω)x = (1 − H2(ω)H(ω))x

which is also a complex exponential. Since y = H1(ω)u, it must be that

y = H1(ω)(1 − H2(ω)H(ω))x

Since y = H(ω)x,

H(ω)x = H1(ω)(1 − H2(ω)H(ω))x

Eliminate x and solve for H to get

H(ω) = H1(ω)/(1 − H2(ω)H1(ω))

when (1 − H2(ω)H1(ω)) is not zero. This gives the frequency response of the feedback system in terms of those of the component systems.