• Home
•  Up to Topics
•  Previous
•  Next

Week 4

• Nondeterminism
• Example
• Model
• Possible updates
• Relations
• Abstraction
• Equivalence
• Simulation
• Deterministic
• Abstraction
• Nondeterministic
• Behaviors
• Theorem
• Not theorem
• Uses
• Bisimulation
• Examples

Simulation and Bisimulation

Consider deterministic state machine A:

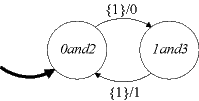
and nondeterministic state machine B:

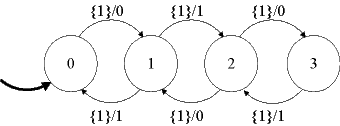
Consider a game, where each machine starts in its initial state. Then, given an input, A reacts, and B tries to react in such a way as to produce the same output (given the same input). For the above examples, B can always do this, so B is said to simulate A. Equivalently, we say that B simulates A.

The game can be turned around, where B makes a move and A tries to match it. In the above examples, this is again possible, so A simulates B. Moreover, in each round of the game, whichever of A or B moves first, the other can match the move. In such circumstances, A and B are said to be bisimilar. Bisimilarity is a strong form of equivalence, stronger than input/output equivalence.

We can track this game by looking at the state responses of the two machines. They each start in their initial state, a fact we can represent with the tuple

( 0and2, 0 ) ∈ States_A × States_B

When the first 1 arrives at the input, the two machines change to

( 1and3, 1 ) ∈ States_A × States_B

Continuing in this fashion, we see that the states of the two machines are always in the set

{ ( 0and2, 0 ), ( 1and3, 1 ), ( 0and2, 2 ), ( 1and3, 3 ) } ⊂ States_A × States_B.

This set is a relation between States_A and States_B, and is called the bisimulation relation. Note that the names of the states in machine A are highly suggestive of this relation.