Polar coordinates
The representation of a complex number as a sum of a real and imaginary number, z = x + iy, is called its Cartesian representation.Recall from trigonometry that if x, y, r are real numbers and r 2 = x 2 + y 2, then there is a unique number θ with 0 ≤ θ < 2π such that
sin(θ) = y / r.
That number is
| θ | = | cos -1(x / r), |
| = | sin -1(y / r) | |
| = | tan -1(y / x) |
We can therefore express any complex number z = x + iy as
| z | = | | z | (x / | z | + iy / | z |) |
| = | | z | (cos θ + i sin θ) | |
| = | | z | e iθ , |
where θ = tan -1(y / x). The angle or argument θ is measured in radians, and it is written as arg(z). So we have the polar representation of any complex number z as
The two representations are related by
and
The values x and y are called the Cartesian coordinates of z, while r and θ are its polar coordinates. Note that r is real and r 3 0.
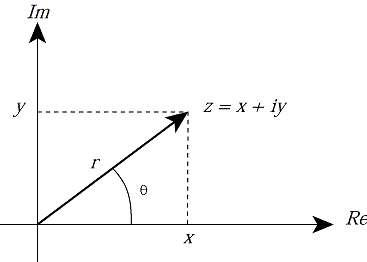
Note that for any integer K,
This is because
and
Thus, the polar coordinates (r, θ) and (r, θ + 2Kπ) for any integer K represent the same complex number. Thus, the polar representation is not unique; by convention, a unique polar representation can be obtained by requiring that the angle given by a value of θ satisfying 0 ≤ θ < 2π or -π < θ ≤ π.
Example 1
| The polar representation of the number 1 is 1 = 1 e i0. Notice that it is also true that 1 = 1 e i2π, because the sine and cosine are periodic with period 2π. The polar representation of the number -1 is -1 = 1 e iπ. Again, it is true that -1 = 1 e i3π, or, in fact, -1 = 1 e iπ + K2π for any integer K. |
Products
Products of complex numbers represented in polar coordinates are easy to compute. If zi = ri e iθi , thenThus, the magnitude of a product is a product of magnitudes, and the angle of a product is the sum of the angles,
arg(z1 z2 ) = arg(z1 ) + arg(z2 )
Example 2
|
We can use the polar representation to find the n distinct roots of the
equation z n = 1. Write z = re
iθ, and 1 = e
i2kπ, so
which gives r = 1 and θ = 2kπ / n, k = 0, 1, ... , n - 1. These are called the n roots of unity. |
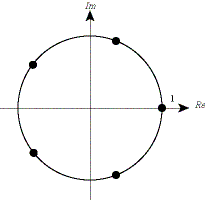
Figure: The 5 roots of unity.
