Multiplying Signals
We have seen that convolution in the time domain corresponds to multiplication in the frequency domain. It turns out that this relationship is symmetric, in that multiplication in the time domain corresponds to a peculiar form of convolution in the frequency domain. That is, given two discrete-time signals x and p with DTFTs X and P, if we multiply them in the time domain,then in the frequency domain,
where the symbol "⊗ " indicates circular convolution, defined by
To verify this, we can substitute into the above integral the definitions for the DTFTs X(ω ) and P(ω ) to get
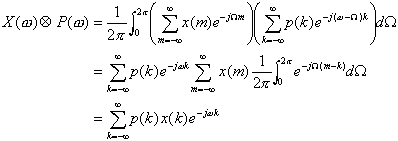
where the last equality follows from the observation that the integral in the middle expression is zero except when m = k, when it has value one. Thus, X(ω ) ⊗ P(ω ) is the DTFT of x(n) p(n), as we claimed.

 Up to Topics
Up to Topics Previous
Previous Next
Next